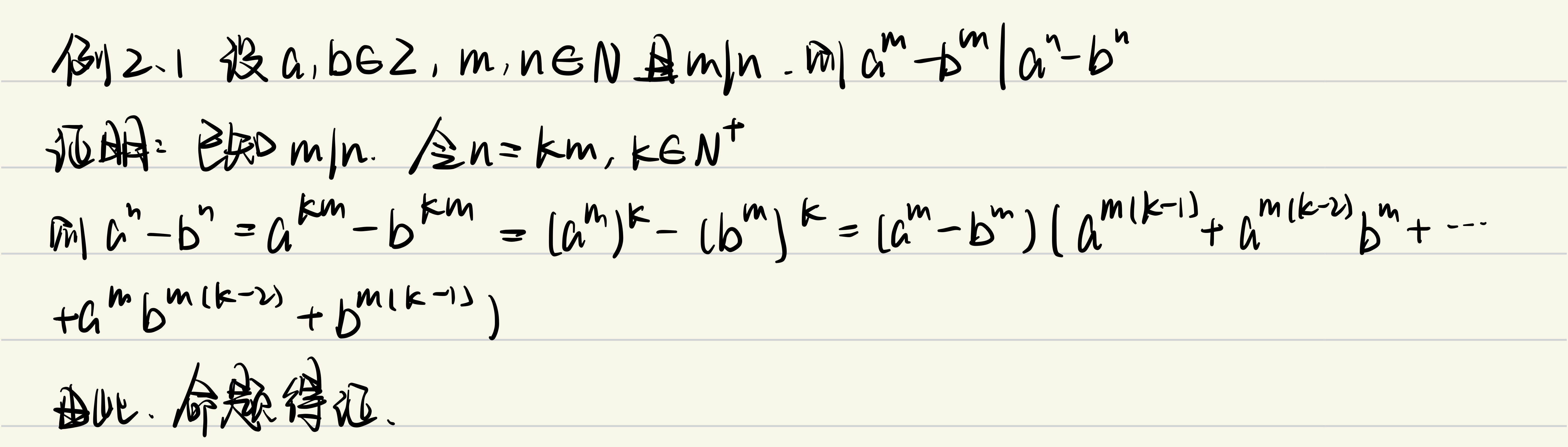初等数论笔记

发布于 2023年6月19日

我会将学习初等数论过程中的所有笔记都整理到这里。使用的教材是哈尔滨工业大学出版社出版的《基础数论入门》。

第 1 章 自然数的基本性质

Peano（皮亚诺）公理

1. $0$ 是自然数；
2. 每一个确定的自然数 $a$，都有一个确定的后继数 $a'$ ，$a'$ 也是自然数；
3. 对于每个自然数 $b$、$c$，$b=c$ 当且仅当 $b$ 的后继数等于 $c$ 的后继数；
4. $0$ 不是任何自然数的后继数；
5. 任意关于自然数的命题，如果证明：它对自然数 $0$ 是真的，且假定它对自然数 $a$ 为真时，可以证明对 $a'$ 也真。那么，命题对所有自然数都真。

其中第 5 条引出了数学归纳法。

一般用 $\mathbb N$ 表示自然数集 $\left\{0, 1, 2,\cdots\right\}$。

（第一）数学归纳法

任给关于自然数 $n$ 的一个命题 $P(n)$, 如果 $P(0)$ 成立，而且对任何自然数 $n$ 只要 $P(n)$ 成立便有 $P(n+1)$ 成立，则命题 $P(n)$ 对所有自然数成立。

例

证明：对任意 $n\in \mathbb N$，都有 $2^n\geq n+1$。

证明：当 $n=0$ 时，$2^0\geq 0+1$ 成立。

假设对 $n$ 有 $2^n\geq n+1$，则 $2^{n+1}\geq 2(n+1)=2n+2\geq (n+1)+1$。

由归纳法，得对任意 $n\in \mathbb N$，都有 $2^n\geq n+1$。

数学归纳法（一般形式）

设命题 $P(m)$ 对于整数 $m\geq m_0(m_0\in \mathbb{Z})$ 有意义。假定 $P(m_0)$ 成立；并且对任何整数 $m\geq m_0$，如果假设 $P(m)$ 成立能够得出 $P(m+1)$ 成立，那么对于整数 $m\geq m_0$ 总有 $P(m)$ 成立。

（第二）数学归纳法（串值归纳法）

任给关于自然数 $n$ 的一个命题 $P(n)$, 如果 $P(0)$ 成立，而且对任何 $n\in \mathbb{N}$ 只要 $P(0),\cdots ,P(n)$ 都成立便有 $P(n+1)$，则命题 $P(n)$ 对所有自然数 $n$ 成立。

证明：令命题 $Q(n)$ 表示 $P(0),\cdots ,P(n)$ 都成立。

对 $n$ 进行归纳。$P(0)$ 成立即 $Q(0)$ 成立。

由第一数学归纳法，由 $P(0), \cdots ,P(n)$ 成立可以得出 $P(n+1)$ 成立。

即由 $Q(n)$ 成立可以得出 $Q(n+1)$ 成立。

由第一数学归纳法，$Q(n)$ 对所有自然数 $n$ 成立。从而命题 $P(n)$ 对所有自然数 $n$ 成立。

最小数原理

自然数集 $\mathbb{N}$ 的任一个非空子集必有最小元。

证明：假设 $\mathbb{N}$ 的一个非空子集 $S$ 没有最小元。

显然，$0\notin S$。（否则 $0$ 就是 $S$ 的最小元。）

假设 $1,2,\cdots ,n\notin S$，则 $n+1\notin S$。（否则 $n+1$ 就是 $S$ 的最小元）

因此 $S$ 为空集，矛盾。因此自然数集 $\mathbb{N}$ 的任一个非空子集必有最小元。

第 2 章 整除性、素数及算数基本定理

整除的定义

对于 $a, b\in \mathbb{Z}$，如果有 $q\in \mathbb{Z}$ 使得 $aq=b$，则称 $a$ 整除 $b$，记为 $a\mid b$。当 $a$ 不整除 $b$ 时，记为 $a\nmid b$。

Eratosthenes（埃拉托色尼）筛法（埃氏筛法）

设 $m, N$ 为正整数，且 $\sqrt{N}<m\le N$，则 $m$ 为素数当且仅当不超过 $\sqrt{N}$ 的素数都不整除 m。

应用

当筛选 $100$ 以内的素数时，先把 $1$ 筛去。接着依次将 $2, 3\cdots$ 的倍数都筛去。由于 $\sqrt{100}=10$，因此只需筛去小于等于 $10$ 的素数之倍数即可。即在这种情况下，只需要筛去 $2, 3, 5, 7$ 的倍数，剩下的就都是素数了；）

Eratosthenes（埃拉托色尼）筛法（埃氏筛法）

证明：若 $m$ 为素数，则它没有真因子，

从而不被不超过 $\sqrt{N}$ 的素数所整除。

若 $m$ 为合数，则存在 $p$、$q$ 使得 $m=pq$，且有 $p\leq q$。

因此 $m$ 被不超过 $\sqrt{N}$ 的素数 $p$ 所整除。

因此 $m$ 为素数当且仅当不超过 $\sqrt{N}$ 的素数都不整除 m。

算数基本定理（整数的唯一分解定理）

任何大于 $1$ 的整数 $n$ 可表示成有限个（可重复）素数的乘积。当不考虑乘积中因子的顺序时这种分解是唯一的。

根据以上定理，大于 $1$ 的整数 $n$ 可以唯一地表示为 ${p_1}^{\alpha_1}\cdot \cdots \cdot {p_r}^{\alpha_r}$ 的形式，其中 $p_1 <\cdots <p_r$ 为不同素数，$\alpha_1,\cdots ,\alpha_r$ 为整数。

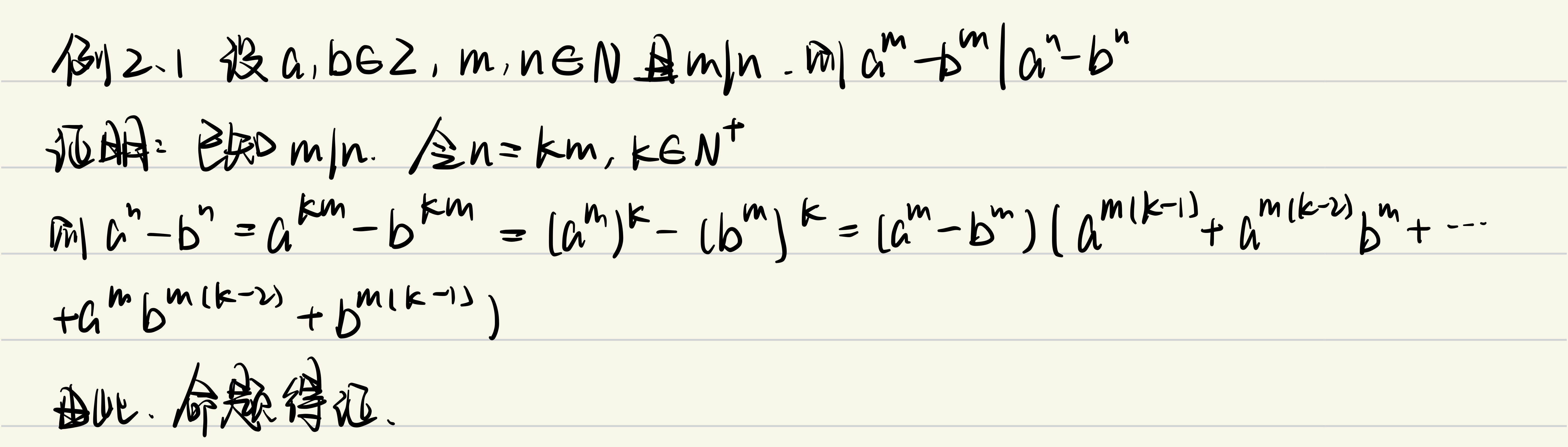
第三章 带余除法、最大公因数及最小公倍数

带余除法

设 $a, b\in \mathbb Z$ 且 $b\neq0$，则有唯一的 $q, r\in \mathbb Z$ 使得

证明：（存在性）令 $a+bZ=\left\{a+bx\right\}$，

由 $b\neq0$ 可知，$\left(a+bZ\right)\cap N\neq \varnothing$，

由最小数定理，$\left(a+bZ\right)\cap N$ 有最小元，

记为 $r=a-bq, q\in \mathbb Z$，可证 $0\leq r<\left|b\right|$，

$q$，$r$ 即为所有。

最大公因数

设 $a_1,\cdots ,a_n\in \mathbb Z$，$a\in \mathbb Z$，若对于任意的 $i$，有 $a|a_i$，则称 $a$ 为 $a_1,\cdots ,a_n$ 的公因（约）数。

若 $d\in \mathbb N$ 是 $a_i$ 的公因数，且 $a_i$ 的任何公因数都整除 $d$，则称 $d$ 为 $a_1,\cdots ,a_n$ 的最大公因数，记为 $d=(a_1,\cdots, a_n)$。

若 $a_1=\cdots=a_n=0$，则 $(a_1,\cdots,a_n)=0$；

若 $a_i$ 不全为 $0$，则 $(a_1,\cdots,a_n)=\max\left\{\text{所有的公因数}\right\}$

公因数是最大公因数的因数，最大公因数是公因数的倍数。

最大公因数可由 $a_i$ 线性表出，即 $d=a_1x_1+\cdots+a_nx_n$，其中 $x_i$ 不唯一，可由辗转相除法得出。

最小公倍数

设 $a_1,\cdots ,a_n\in \mathbb Z$，$a\in \mathbb Z$，若对于任意的 $i$，有 $a_i|a$，则称 $a$ 为 $a_1,\cdots ,a_n$ 的公倍数。

若 $m\in \mathbb N$ 是 $a_i$ 的公倍数，且 $m$ 整除 $a_i$ 的任何公倍数，则称 $m$ 为 $a_1,\cdots ,a_n$ 的最小公倍数，记为 $m=[a_1,\cdots, a_n]$。

若 $a_i$ 中有 $0$，则 $[a_1,\cdots,a_n]=0$；

若 $a_i$ 都不为 $0$，则 $[a_1,\cdots,a_n]=\max\left\{\text{所有}\textbf{正}\text{的公倍数}\right\}$

公倍数是最小公倍数的倍数，最小公倍数是公倍数的因数。